Hinweise zum Datenschutz

*
Nebelfilter visuell
Von der Transmissionskurve zur visuellen Wahrnehmung

Nebelfilter zeigen in der Praxis unterschiedliche Resultate, auch dann, wenn sie nominell zur selben Filterklasse gehören. Insbesondere die Unterschiede bei der visuellen Beobachtung werden unter interessierten Sternfreunden mit großem Interesse betrachtet und oft auch leidenschaftlich diskutiert. Insbesondere zeigt die praktische Erfahrung, dass vor allem unterschiedliche Bedinungen zu sehr unterschiedlichen Bewertungen desselben Filters führen. Störlicht durch Lichtverschmutzung spielt als Grund dafür die größte Rolle. Wie sich ein Filter aber visuell verhält, lässt sich aus der Transmissionskurve nur schlecht ablesen und bisher gab es zur Erklärung der unterschiedlichen Filtereigenschaften nur rudimentäre Ansätze.
In diesem Artikel wird eine Möglichkeit vorgestellt, mit der sich herkömmliche Transmissionskurven so aufbereiten lassen, dass konkrete Aussagen über das Filtervehalten bei der visuellen Beobachtung gewonnen werden können. Dies soll nicht nur eine Brücke zwischen Theorie und Praxis schlagen, sondern vielmehr auch eine bessere Grundlage zur Diskussion und Bewertung von Transmissionskurven schaffen.

Bestimmend für das Verhalten eines Filters ist in erster Linie dessen Fähigkeit zur Unterdrückung von Störlicht vom Himmelshintergrund bei gleichzeitig maximaler Transmission des gewünschten Lichts vom Beobachtungsobjekt. Im Ergebnis soll ein Filter also das Verhältnis zwischen Störlicht und Objektlicht verbessern. Bei visueller Beobachtung ist aber neben diesem Verhältnis die absolute Transmission nicht zu vernachlässigen, da das menschliche Auge eine schwächere Transmission von “Nutzlicht” nicht ausgleichen kann, so wie das bei der Fotografie durch eine verlängerte Belichtungszeit möglich ist.
Der Wahrnehmung des Objekts durch den Beobachter liegt außerdem nicht allein die Transmissionskurve des Filters zugrunde, sondern auch die Empfindlichkeitskurve des menschlichen Auges, und zwar in diesem Fall speziell die Empfindlichkeitskurve für das dunkeladaptierte Auge (skotopisches Sehen).
Die Kombination beider Kurven ermöglicht es, die verschiedenen Durchlassbereiche eines Filters miteinander zu vergleichen und so zu bewerten. Eine Transmission des Filters von 100% bei 656nm (H-Alpha-Licht)  im Vergleich zu 10% bei 501nm (OIII-Licht) bedeutet, die 100% für H-Alpha Licht mit 0,04% Empfindlichkeit des dunkeladaptierten Auges zu mutltiplizieren. Also als Produkt geschrieben 1*0,0004=0,0004, also 0,04% für H-Alpha und bei OIII entsprechend 96% Empfindlichtkeit und 10% Transmission nun 0,1*0,96=0,096 also 9,6%. Mit einem solchen Filter müsste also eine H-Alpha-Lichtquelle 240 mal heller sein, als eine [OIII]-Lichtquelle, damit beide gleich hell “aussehen”.

Damit lassen sich zwei Leistungswerte des Filters als wesentlich für die Filtereigenschaften herausstellen:

1. Filtertransmission auf den gewünschten Wellenlängen (Linien) von Emissionsnebeln.

Welche Wellenlängen erwünscht sind, ist in der Praxis objektabhängig, da nicht alle Objekte alle Linien gleich stark ausstrahlen. Einige spezielle Objekte zeichnen sich durch das Fehlen oder nur vergleichsweise schwache Vorhandensein einer oder mehrerer Linien aus. Für die visuelle Beobachtung von Interesse sind dabei in der Praxis fast ausschließlich die drei Linien H-Beta (486,1nm), OIII (500,7nm) und die weitere OIII-Linie bei 495,9nm. Für diese Linien werden zur Bewertung untereinander die typischen Intensitätsverhältnisse für diffuse und planetarische Nebel  übernommen.

Um dies zu differenzieren sind im Anhang auch Beispiele für einzelne Objekte mit genauen Daten über die Verhältnisse zwischen diesen Emissionslinien angegeben.

2. Absorption bzw. Wahrnehmbarkeit unerwünschter Wellenlängen (Störlicht, Himmelshintergrund).

Unerwünschtes Licht, also Störlicht oder im weitesten Sinne Himmelshintergrund, wird natürlich ebenso vom Auge unterschiedlich wahrgenommen. Die Gewichtung der unterschiedlichen Wellenlängen (= Farben) erfolgt dabei ganz genauso mittels der Empfindlichkeitskurve des dunkeladaptierten Auges. Dabei berücksichtigt wird jedoch die unterschiedliche Intensität des Störlichts, so dass eine weitere Kurve, nämlich die Intensitätskurve für Störlicht in die Berechnung eingeht. Eine zuverlässige Aussage über die Störlichtunterdrückung lässt sich aus dem Vergleich dieser Kurve mit derselben Kurve ohne Filter - was 100% Transmission auf allen Wellenlängen bedeutet - erzielen.

Die Ergebnisse dieser Auswertung zeigen eine signifikante Übereinstimmung mit den Beobachtungsergebnissen in der Praxis, was vor allem die Störlichtunterdrückung der Filter angeht. Man erkennt aber auch überraschend geringe Unterschiede der absoluten Filtertransmission, die in der Praxis deutlich wahrnehmbare Unterschiede verursachen.

Kombination von Filtertransmission, Störlichtemission und skotopischer Empfindlichkeit

Grundlage der folgenden Berechnungen sind die Transmissionsmessungen zu verschiedenen Nebelfiltern, die entweder aus eigenen Messungen (Danke an Christian Brinkmöller und Kai Richter)  oder aus dem Archiv von André Knöfel [3] stammen. Betrachtet wurden die Kurven in 1nm Schritten. Eventuelle Ungenauigkeiten durch die Datenreduktion von z.B. 1/10nm Auflösung ändern das Ergebnis nur marginal und erscheinen ohnehin im Rahmen der Messgenauigkeit hinnehmbar.
Weiteren Eingang fand die skotopische Empfindlichkeitskurve des menschlichen Auges nach CIE Proceedings [1], die ebenfalls in 1nm Schritten gegeben und seit 1991 ISO-Standard ist.
Die Intensitätskurve für typisches Störlicht wurde zurückgerechnet aus einer aus [2] entnommenen Kurve. Dadurch entstandene Ungenauigkeiten erscheinen, nicht nur in Ermangelung einer besseren Quelle, sondern auch wegen zu erwartender Abweichungen je nach Standort, akzeptabel.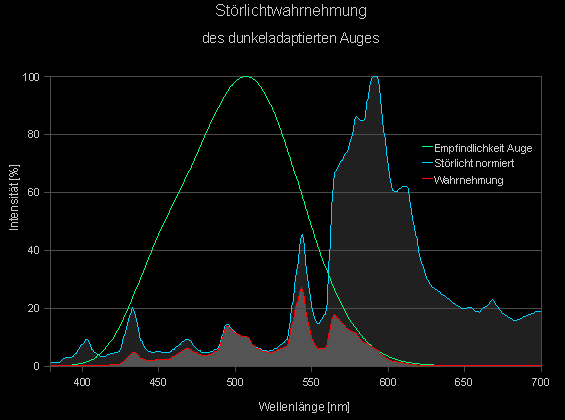

Empfindlichkeit des dunkeladaptierten Auges (grün) und Störlichtintensität (blau) bestimmen die Wahrnehmung von Störlicht (rot).

Die Gewichtung der Störlicht-Intensitätskurve mit der Empfindlichkeitskurve ergibt die Wahrnehmungskurve für Störlicht, und die unter dieser Kurve eingeschlossene Fläche S_N entspricht der ohne Filter wahrgenommenen Störlichtintensität. Zur Flächenberechnung wurden in Anlehnung an das Riemann-Integral die Intensitätswerte der Wahnehmungskurve für jeden Nanometer aufaddiert.
Die Verwendung  der so geschaffenen Wahrnehmungskurve für Störlicht zur Gewichtung der Transmissionskurve eines Filters zeigt die Restintensität des noch wahrnehmbaren Störlichts, wiederum als Fläche S_F unter der entstehenden Kurve. Das Verhältnis S_N/S_F der beiden Flächen, also der wahrgenommenen Störlichtintensität mit und ohne Filter, kann nun einfach als Prozentwert interpretiert werden (S_N/S_F* 100). Abgezogen von 100% ergibt sich die Störlichtunterdrückung des Filters in Prozent bei dunkeladaptiertem Auge.

Der Lumicon UHC erzielt für den visuellen Beobachter eine Störlichtunterdrückung von 85%

Bewertung der Transmissionseigenschaften

Zur Bewertung der Transmissionseigenschaften werden die drei für visuelle Beobachter wesentlichen Linien von Emissionsnebeln herangezogen, nämlich H-Beta bei 486,1nm, [OIII] bei 495,9nm und [OIII] bei 500,7nm. Deren Intensitätsverhältnis ist je nach Objektklasse unterschiedlich. Einzelne Objekte bzw. sogar unterschiedliche Regionen einzelner Objekte weichen zwar deutlich von den üblichen Werten ab, es geht aber um ein Gesamtbild, das durch die folgenden Verhältnisse wiedergegeben wird: [5], [4]

Außerdem muss wiederum die spektrale Empfindlichkeit des dunkeladaptierten Auges berücksichtigt werden. Sie beträgt für H-beta 86,2%, für [OIII] bei 495,9nm 95,7% und bei 500,7nm 98,6%. Damit werden die Tabellenangaben multipliziert.
Insgesamt ergibt sich für Diffuse Nebel eine Gewichtung (Hß, [OIII], [OIII]) von 0,862 zu 1,972 zu 0,71775 . Dies aufsummiert ergibt einen Maximalwert von 3,55175, der die maximal wahrnehmbare Intensität eines durchschnittlichen diffusen Nebels ausdrückt. Für planetarische Nebel kommt man auf  0,862 zu 11,832 zu 3,828 und insgesamt 16,522.
Die Transmissionswerte des jeweiligen Filters für diese Wellenlänge werden mit deren Gewichtung multipliziert und von diesen Maximalwerten abgezogen. Dargestellt in Prozent ergibt sich der Verlust an Nebelhelligkeit durch den Filter, bzw. als umgekehrter Wert die wahrnehmbare Resthelligkeit nach Verlusten durch den Filter.
Insbesondere weicht diese Bewertung der Filter vom normalen Begriff der “selektiven Transmission” ab, und zwar insofern, als sich die selektive Transmission auf das gewünschte Passband des Filters bezieht und nicht ausschließlich auf die darin enthaltenen Nebellinien. Hinzu kommt die Wichtung der Linien nach der Empfindlichkeitskurve des Auges. Man erhält so auch einen wesentlich aussagekräftigeren Wert, als mit der gebräuchlichen Angabe einer Halbwertsbreite. Insbesondere berücksichtigt die Halbwertsbreite weder einen Versatz der maximalen Transmission zur gewünschten Linie, noch den in der Realität praktisch immer von der idealen Sinusform abweichenden Kurvenverlauf.

Speziell bei reinen Linienfiltern gibt es die Besonderheit, dass entweder die H-Beta-Linie ([OIII]-Filter)oder die beiden [OIII]-Linien (H-Beta-Filter) nicht erwünscht sind. Bei den in der folgenden Grafik mit einem Sternchen gekennzeichneten Einträgen ist diese Transmission dann nicht berücksichtigt. Dieselben Filter ohne Sternchen sind mit allen Linien bewertet. Diejenigen [OIII]-Filter, bei denen es keinen Eintrag mit Sternchen gibt, haben keine bemerkenswerte Transmission auf der H-Beta-Linie, so dass diese Differenzierung keinen Unterschied macht. Für den visuellen Beobachter ist im Normalfall die Bewertung ohne Sternchen der wesentliche Wert. Nur wenn innerhalb eines Objekts die Betrachtung von beispielsweise [OIII]-Strukturen durch anders strukturierte H-Beta-Strukturen (oder umgekehrt) gestört wird, kann die Bewertung mit Sternchen überhaupt praxisrelevant werden.

Um eine Gesamtübersicht zu vermitteln, wurde außerdem die Störlichtwahrnehmung durch den vermessenen Filter in Prozent dargestellt. Dazu noch der Hinweis, dass Störlichtwahrnehmung und Nebelwahrnehmung immer vom Objekt und den Gegebenheiten am Beobachtungsort abhängen. So lässt sich aus dem Diagramm keine “Kontrastverbesserung” oder ein ähnlich direkter Wert ablesen. Dazu müsste die Objekthelligkeit und die visuelle Helligkeit des Himmelshintergrundes am Beobachtungsplatz und natürlich für die Himmelsregion des Beobachtungsobjekts bekannt sein. Wegen der logarithmischen Wahrnehmung von Lichtintensitäten ist auch die verwendete AP zu beachten. Es sei die Bemerkung erlaubt, dass in dem Falle das “hingucken” einfacher zu realisieren ist, als eine Vorausberechnung!
Besonders wichtig ist der Blick auf die Störlichtwahrnehmung (rot). Auch geringe Unterschiede sind durchaus wahrnehmbar und die Leistung der Linienfilter lässt sich hauptsächlich an diesem Wert ablesen.
Ein kurzer roter Balken steht also für eine gute Störlichtdämpfung und ist somit unter Bedingungen mit spürbaren Störlicht, also mindestens bis 6mag visuelle Grenzgröße, die wichtigste Eigenschaft des Filters. Lange Balken in grün und blau stehen für wenig Dämpfung des Nebellichts und sind vor allem unter dunklem Himmel, also ab 6mag aufwärts, wesentlich. Ihr Verhältnis zueinander spiegelt die Eignung für H-Beta-Objekte wieder. Ist der grüne Balken länger als der blaue, so liegt das an einer schlechteren H-Beta-Transmission, so dass der Filter bei Objekten mit bemerkbarem H-Beta-Anteil gehandicapt ist.

Nebelfilter im Überblick. Besonders bei der Störlichtwahrnehmung (roter Balken) sind schon geringe Unterschiede spürbar.

Weitere Aspekte

Die Berechnung der Transmission gilt für senkrechten Lichteinfall. Das allerdings ist nur auf der optischen Achse der Fall. Abseits der optischen Achse gibt es Verschiebungen der Transmissions-Peaks zum Blauen hin. Dadurch verändern sich an besonders schnellen Optiken (f/4) die Filtereigenschaften geringfügig. Da aber die Bewertung nicht nur für spezielle Teleskope gelten soll, kann dies nicht berücksichtigt werden. Es spielt auch in der Praxis eine sehr untergeordnete Rolle.

Die optische Qualität des Filters wird hier natürlich nicht erfasst. Eine schlechte Politur, Verspannungen des Filterglases oder auch Doppelreflektionen bei Filtern mit mehreren beschichteten Flächen, zum Beispiel solche mit zwei verkitteten Filtergläsern, können die optischen Eigenschaften verschlechtern und im Bild stören. Auch das kann nur die Praxis zeigen.

Deepsky Filter

Bei den betrachteten Deepsky-Filtern zeigt sich ein recht einheitliches Bild im Bereich der gewünschten Transmission. Lediglich der Seben CLR fällt durch schlechte Transmission bei H-Beta auf. Bei der Störlichtdämpfung fällt auf, dass IDAS, Skyglow und Astronomik CLS sehr viel Störlicht zwischen 540nm und 550nm passieren lassen. Der Baader Skyglow, kein Deepsky-Filter und hier nur wegen seiner Verbreitung und der verwechselbaren Namensgebung aufgeführt, kann kaum 40% des Störlichts ausblenden.

UHC Filter

Bei den UHC-Filtern zeigt sich, dass bei einigen Fabrikaten die Störlichtdämpfung kaum stärker ausfällt, als bei kräftiger wirkenden Deepsky-Filtern. Das ist besonders auffällig beim Baader UHC-S, der 31,5% Störlicht wahrnehmbar werden lässt und damit etwas mehr, als Seben CLR und Meade Nebular Broadband.

[OIII]-Filter

Bei den [OIII]-Filtern lässt sich das wahrnehmbare Störlicht bereits sehr gut an der Halbwertsbreite ablesen und die Filterkurven finden sich quasi wie nach ihrer Halbwertsbreite “aufgereiht”. Beim TeleVue OIII fällt die geringe Flankensteilheit auf und mit seinem Wert von 17,42% lässt er mehr bzw. etwa gleich viel Störlicht passieren, wie Lumicon UHC und  Meade Narrowband.

Ausblick

Fotografisch interessierte können anstelle der skotopischen Empfindlichkeitskurve ähnliche Rechnungen mit der Empfindlichkeitskurve von CCD-Sensoren oder Filmmaterial anstellen. Da aber bei monochromen CCD-Sensoren die Empfindlichkeitskurven deutlich ausgeglichener sind, als die des menschlichen Auges, ergeben sich weniger starke Unterschiede zur normalen Transmissionskurve. Anders ist dies jedoch bei Farb-CCD-Sensoren, bei denen sich durch die Farbfilter spürbare Unterschiede ergeben.

Anhang Signalverbesserung

Unter Umständen ist es auch von Interesse, wie gut ein Filter das Signal aufwertet, wie sehr also der Bildvordergrund gegenüber dem Bildhintergrund hervorgehoben wird. Linienfilter sollten hier die besten Werte haben, da diese je “nur” die gewünschte Linie passieren lassen müssen, während alle anderen Filter auf breitere Durchlassbereiche abgestimmt sind. Interessant ist aber der Vergleich innerhalb der Filterklassen. Da eine starke Störlichtdämpfung meist auch mit einer stärkeren Dämpfung des gewünschten Nebellichts einher geht, stellt sich die Frage, bei welchem Filter beides in optimalem Verhältnis steht. Die folgende Grafik basiert auf dem Quotienten aus Nutzlicht zu Störlicht, bezüglich der oben angegebenen Werte Störlichtwahrnehmung und zum einen der Wahrnehmung von planetarischen Nebeln und  zum anderen jener von diffusen Nebeln. Höhere Werte sind somit also besser, jedoch unter der Annahme, dass der Nebel nicht insgesamt zu dunkel wird. Die Grafik zeigt nicht, dass der hier in Führung liegende Baader OIII mindestens 15% weniger Nebellicht passieren lässt, als der Lumicon OIII. Der Baader OIII ist also nur dann der bessere Filter, wenn starkes Störlicht seine starke Filterwirkung erforderlich macht und der Nebel nicht so schwach ist, dass der Helligkeitsverlust durch den Filter ihn unter die Wahrnehmungsschwelle drückt.

Der Quotient aus Nebelwahrnehmung und Störlichtwahrnehmung zeigt das Verbesserungspotenzial der Filter
unter der Bedingung, dass das Objekt hell genug ist und der Himmelshintergrund den Filter auch erfordert.

Anhang

Beispiele für die Intensitätsverhältnisse von Emissionslinien in Gasnebeln

Referenzen:

[1] CIE Proceedings (1951), Vol. 1, Sec 4; Vol 3, p. 37, Bureau Central de la CIE, Paris, 1951

[2] The Journal of Experimental Biology 209, 789-800, The Company of Biologists 2006,
 Sönke Johnsen et al., Crepuscular and nocturnal illumination and its effects on color perception by the nocturnal hawkmoth Deilephila elpenor

[3] Transmissionskurven von Filtern, André Knöfel, http://www.astroamateur.de/filter/

[4] unter Anderem:

On The Chemodynamics of Wolf-Rayet Ring Nebula: NGC 6888
César Esteban and José M. Vílchez
The Astrophysical Journal, 390:536-540,1992 May 10

Spatial and Spectral Interpretation of a Bright Filament in the Cygnus Loop
J.C. Raymond, et al.
The Astrophysical Journal, 324:869-892,1988 January 15

Ionization and Abundances in the Dumbbel Nebula
Steven A. Hawley and Joseph S. Miller
Publications of the Astronomical Society of the Pacific, 90:39-44, February 1978

[5] Nebular Filters in Deepsky Astronomy
Owen Brazell
Journal of The British Astronomical Association, 104, 5, 1994

[6] A Catalog of Relative Emission Line Intensities Observed in Planetary and Diffuse Nebulae
James B. Kaler
The Astrophysical Journal Supplement Series, 31:517-688, August 1976

[7] Pic du Midi Observatory - T60 Mission
www.astrosurf.com/~buil/us/mission2/mission2.htm#SPECTRUM%20OF%20NGC%201499

Was ist eine Transmissionskurve?

Unter einer Transmissionskurve versteht man eine Darstellung der Lichtdurchlässigkeit des Filters für verschiedene Farben. Von links nach rechts findet man hier kontinuierlich die Lichtfarben von violett über blau grün und gelb bis rot angeordnet. Manche Kurven schließen links davon noch den Bereich des unsichtbaren ultravioletten Lichts und rechts davon den ebenso unsichtbaren Bereich des infraroten Lichts (TV-Fernbedienungen) ein. Als Einheit dient die Wellenlänge des Lichts, mit violettem Licht an der Grenze zu Ultraviolett bei 400nm und tiefrotem Licht an der Grenze zum Infrarot bei 700nm.
Die Höhe der Kurve gibt die Lichtdurchlässigkeit für die entsprechende Wellenlänge - also Farbe - an, meist angegeben in Prozent.

zurück zum Artikel

* Überarbeitung am 2.12.2018: Anhang Signalverbesserung